A.K.A. predictors, features, input variables, the Xs (by their common symbol), RHS (right-hand side of the equation) or, sometimes, just variables as shorthand. Depending on the analysis method or a data scientist’s background, these terms are used interchangeably.

Independent variables are represented by the symbol X. Multiple independent variables are denoted by X~1:n, where n is the number of independent variables.

Contents

1. Intuitively
2. Mathematically

Intuitively,

The meaning rests in the name: these variables are independent contributors to explaining changes in the output variable (A.K.A. dependent variable, response, etc.) - like jigsaw pieces to a puzzle. These are called independent in relation to a output variable. Here, the output variable is an observed quantitative phenomenon that we want to break down, whose understanding is dependent on the independent variables.

Let’s say that (from the below image) you want to understand how much each person contributes to the movement of the cart or, which person moves the cart the most/least. A simple version of this model will include each person as an independent variable and the cart as the dependent variable. It is the effort of the independent Xs that is moving the dependent cart Y. Without the independent variables, the cart will not move.

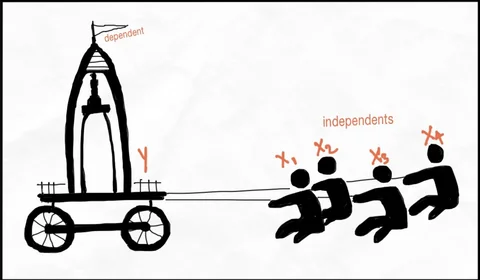
Mathematically,

Suppose that we have a quantitative phenomenon (usually denoted by Y) with n different predictors \((X1, X2, ..., Xn)\), it can be denoted, in its simplest form, as so:
\(Y = f(X~1~, X~2~, ..., X~n~) + e\)

where, \(f()\) is a function, i.e., the relationship between the independent variables, \(e\) is the error margin (the noise, randomness in the modelling since nothing is certain). Here, X1:n explain some systematic information about Y (why Y changes, by how much, etc.).

Let’s take another example to better understand \(e\), the error margin in all models: income (Y) may be explained by predictors like: years of education and work experience (X1 & X2). Here, the error margin, e, would involve edge cases or other predictors that haven’t been included in the model (like, national standard of living, job type, etc.). Usually, the reason for not including key predictors in the model is data availability or quality reasons.